Notes for Piston in a Sphere

updated 2021-07-18

The previous post on this page highlighted what seemed to be two discrepancies (check commit 46c11ec..), the first being a potential typo in equation 12.98, which described \(\frac{\partial}{\partial \theta} P_n(cos \theta)\) . Upon closer inspection I realised there was no typo, and it was an interpretational error on my part.

However, discrepancy 2) related to a difference in m and n index order between the equations in the book and the Mathematica code implementation. This post dives into more detail.

The m and n index order discrepancy

I. Expectations from substitutions

The solution for \(K_{mn} = \int^{\pi}_{\alpha} P_{n}(\cos\theta) P_{m}(\cos\theta)\sin\theta\:d\theta\) (eqn. 12.107) is given in App.II, eqn. 70. In the case where \(m \neq n\), the solution is:

\[\frac{sin\:\alpha( P_{m}(cos\:\alpha)P^{\prime}_{n}(cos\:\alpha) - P_{n}(cos\:\alpha)P^{\prime}_{m}(cos\:\alpha))}{m(m+1) - n(n+1)}\]

Which we’ll visually re-arrange for better comparison after substitution:

\[\frac{sin\:\alpha}{m(m+1) - n(n+1)}\bigg( P_{m}(cos\:\alpha)P^{\prime}_{n}(cos\:\alpha) - P_{n}(cos\:\alpha)P^{\prime}_{m}(cos\:\alpha) \bigg)\]

Where \(P_{n}(cos \:\theta)\) is the Legendre polynomial of order n , and \(P^{\prime}_{n}(cos\:\theta)\) (eqn. 12.98) is:

\[ \begin{align}\begin{aligned}P^{\prime}_{n}(cos \theta) = \frac{\partial}{\partial \theta}P_{n}(cos \theta) = - \frac{n(n+1)}{(2n+1)sin \theta}(P_{n-1}(cos \theta) - P_{n+1}(cos \theta))\\= \frac{n(n+1)}{(2n+1)sin \theta}(P_{n+1}(cos \theta) - P_{n-1}(cos \theta))\end{aligned}\end{align} \]

When we do the substitutions for \(P^{\prime}_{n}(cos\:\alpha)\), \(P^{\prime}_{m}(cos\:\alpha)\) (Appendix II, eqn.70) and \(\theta = \alpha\), the full term is expected to be:

\[\begin{split}\frac{sin\:\alpha}{m(m+1) - n(n+1)} \\ \left( P_{m}(cos\:\alpha)\frac{n(n+1)}{(2n+1)sin\:\alpha}(P_{n+1}(cos\:\alpha) - P_{n-1}(cos\:\alpha)) \\ - P_{n}(cos\:\alpha)\frac{m(m+1)}{(2m+1)sin\:\alpha}(P_{m+1}(cos\:\alpha) - P_{m-1}(cos\:\alpha)) \right)\end{split}\]

As of now the beamshapes piston in a sphere implementation follows the above equation.

II. The textbook code implementation

The code implementation used to generate Fig. 12.23 has the equivalent of:

\[\begin{split}\frac{sin\:\alpha}{m(m+1) - n(n+1)} \\ \left( P_{n}(cos\:\alpha)\frac{m(m+1)}{(2m+1)(sin\:\alpha)}(P_{m+1}(cos\:\alpha)-P_{m-1}(cos\:\alpha)) \\ - P_{m}(cos\:\alpha)\frac{n(n+1)}{(2n+1)(sin\:\alpha)}(P_{n+1}(cos\:\alpha)-P_{n-1}(cos\:\alpha)) \right)\end{split}\]

The m and n indices have been switched in the \(P_{m/n}(cos\:\alpha)\) and the \(P^{\prime}_{m/n}(cos\:\alpha)\) terms – but the \(m(m+1) - n(n+1)\) denominator term remains the same order as in section I .

III. Comparing directivity patterns from sections I and II

The switch in m and n indices between II and III for leads to different directivity patterns - here ka=1 and ka=3 is shown.

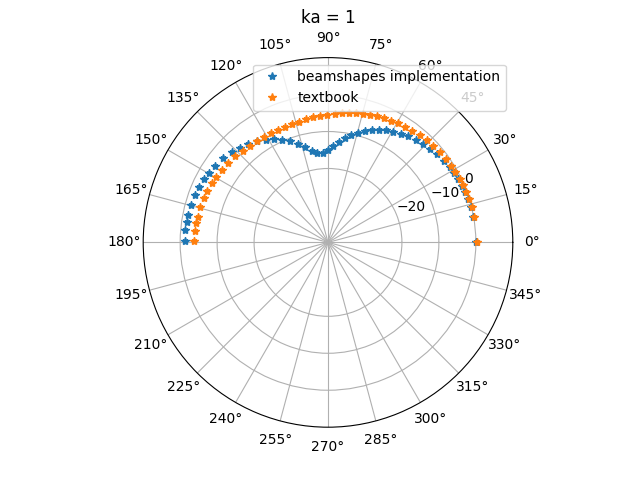
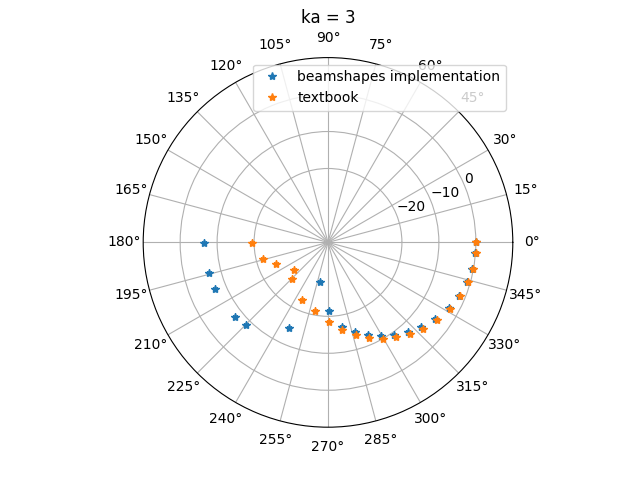
Perhaps the current beamshapes implementation is the result of a coding error? Unlikely, as switching the order of the \(P_{m/n}\) and \(P^{\prime}_{m/n}\) terms in the beamshapes implementations recreates Fig. 12.23 (not shown here).

IV. The correct solution is the Mathematica code implementation

The code implementation is the correct solution - Tim Mellow has checked its correctness also through numerical integration. The current implementations of the piston in a sphere are based on the Mathematica code implementation.

Acknowledgements

Thanks to Tim Mellow for clarifying the discrepancy between published and implemented models, and Gaurav Dhariwal for re-checking the math once more.

References

• Chp 12, Beranek, L. L., & Mellow, T. (2012). Acoustics: sound fields and transducers. Academic Press. (also see the online Errata)

• To see code implementations check out the piston_in_sphere documentation